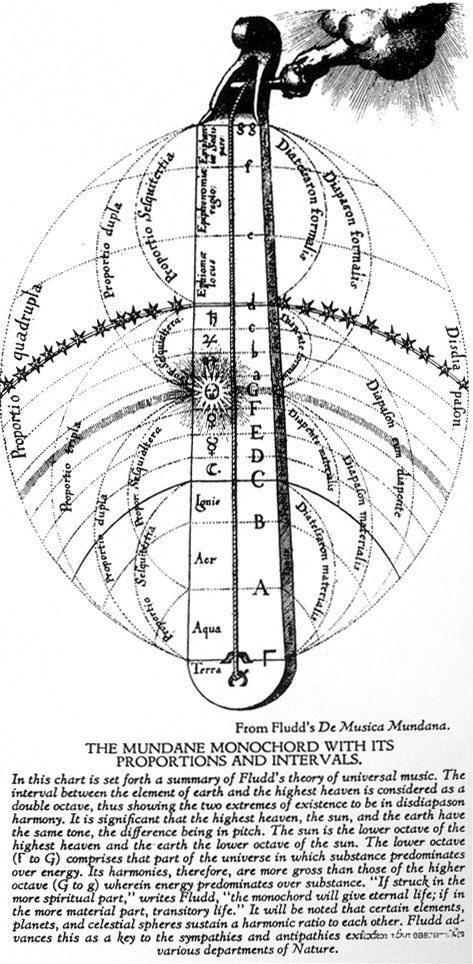
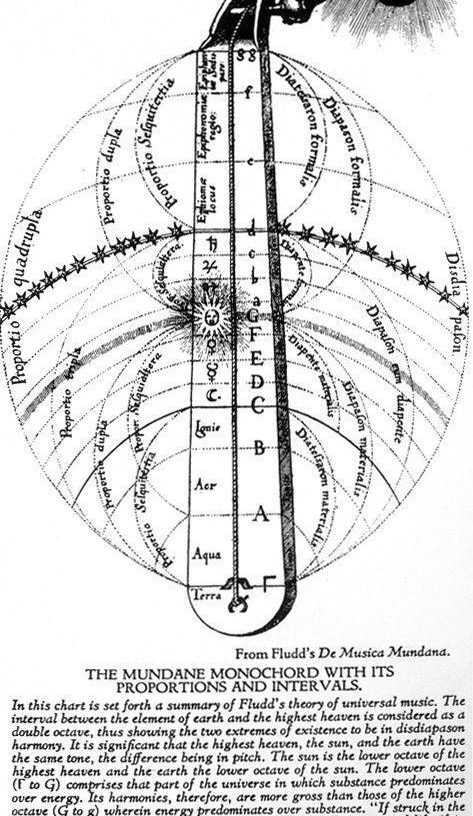
琴弦的嗡嗡声中蕴含着几何,天体的空间中蕴含着音乐。————毕达哥拉斯
音乐发现
毕达哥拉斯发现:里拉(古希腊乐器)和长笛最优美的和弦与弦对应于管的“简单”的长度比例。同时,他也发现了声音频率与上述长度成反比,如弦长缩短一半,频率升高一倍。
毕达哥拉斯是位技艺高超的里拉玩家,他发现当拨动一根长度正好是另一根琴弦的一半的弦时,其音高恰好高了一个八度。他认为不需要实际用耳朵去听,只是选择一个“简单”的数\(1 \leq r \leq 2\)成员基础频率(如220Hz)所产生和和声都能都好听:
频率的3/2倍对应纯5度(Perfect Fifth);频率的4/3倍对应纯4度(Perfect Fourth);频率的8/5倍对应大6度音程(Major Sixth);
数学规律
这些不同频率(有理数倍数)的声音被称为泛音列(overtone series)或谐波列(harmonic series)。有理数倍数的声音好听的原因在于,耳朵能较容易的识别出这些频率的声音所组合出来的韵律(rhythm)。然而,绝大多数稍复杂的有理数倍数的频率,比如211/192,听上去就很难听,因为耳朵已难以从中识别出规律。
因此,我们不得不只使用“简单”的比例,“简单”的一种度量方法就是把分母限制在10以下的整数,但即便这样,结果也并不总能令人满意。同时,我们发现,有些无理数,只要其离简单有理数很近,其对应的声音也很和谐。
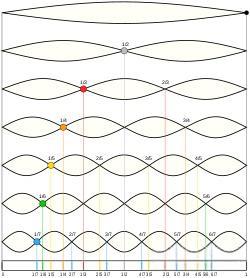
频率驻波
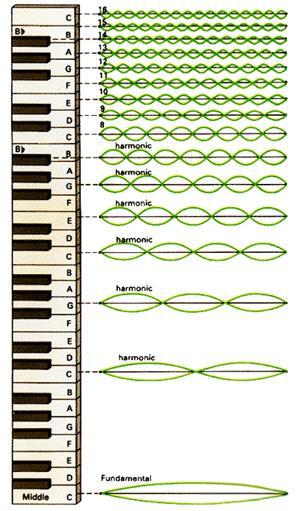
管弦乐存在一种常见的现象,“自然地”产生与它们长度的整数分之一(如1, 1/2,1/3,1/4,1/5,1/6,1/7等)的多个频率,这很类似一种被称为“驻波”的形式,驻就是停止,就是波只是上下振动,而不水平传播,这种弦长是波长整数倍描述的就是这种情形。
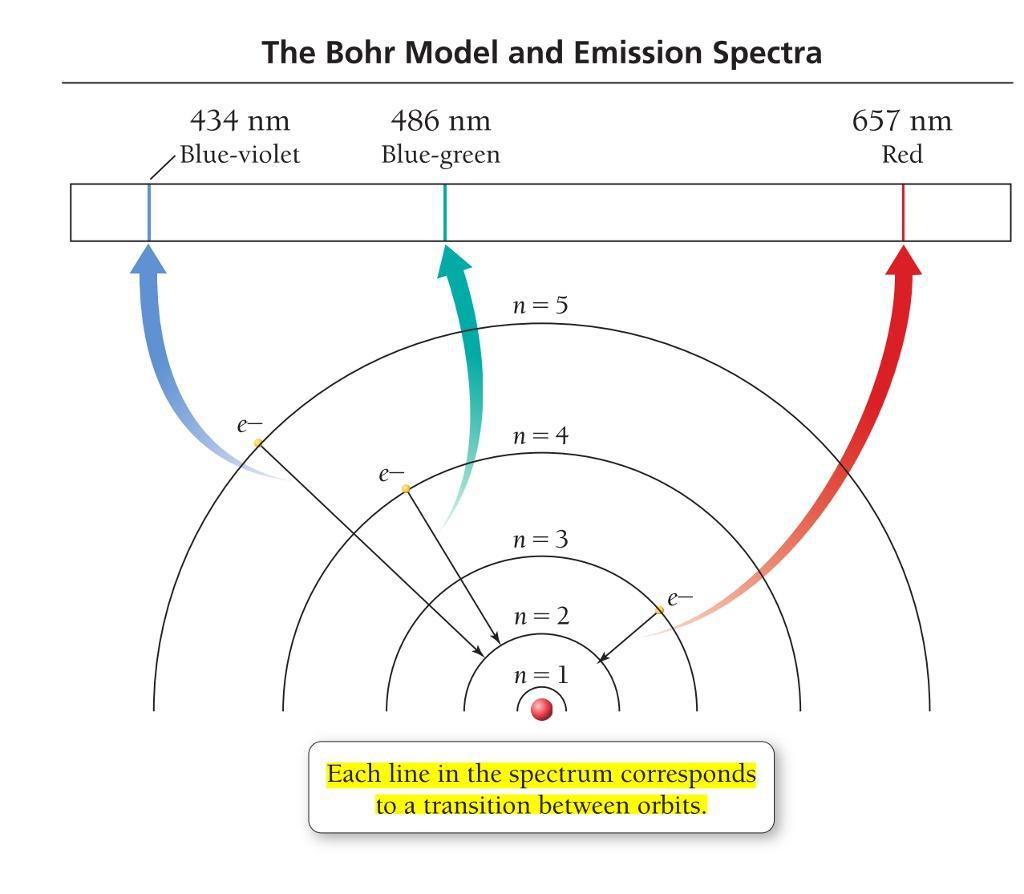
量子频率
波长只能取整数分之一的特点与量子力学中离散的电子轨道的道理是相通的,20世纪初,波尔(Neils Bohr)基于氢原子的光谱提出的原子核模型便是基于此,他发现频率之间的简单关系,比如 \(\frac{3^{2}}{4^{2}}\) 。量子力学与音乐的差别只是以光的颜色频率代替了音符的频率,以 \(\frac{n^{2}}{m^{2}}\) 代替 \(\frac{n}{m}\) ,具体参考巴尔莫公式\(\lambda = \frac{n^{2}}{n^{2}-4}\quad n=3,4,5,\cdots\) 。
天体和音
毕达哥拉斯相信行星和所有的天体的轨道和彼此的距离会发出振动的音符,人类只是缺乏听到这些“天体音乐”的能力,他称之为“天体和音”。