体验
目标
- 理解什么是类别
- 理解成为一个类别的成员意味着什么
- 理解为什么具有单称主项的命题被当作全称命题来处理
- 描述什么是全称肯定命题和全称否定命题
- 解释每种类型的真命题和假命题之间的区别
- 判断哪些句子是每种类型命题的例子
- 使用欧拉圆和文氏图表示每种类型的命题
内容
类别
所谓类别,指的是具有某种独特共同属性的事物的集合。词项指称类别。因此,以下句子表达的是同一个意思:
- 苹果是红色的。
- 具有苹果属性的事物是红色的。
- 苹果是具有红色属性的事物。
- 具有苹果属性的事物也是具有红色属性的事物。
类别可以有很多成员,比如 “狗” 这个类别;但也可以只有一个成员,比如 “亚里士多德” 这个类别。“亚里士多德” 这个类别只有一个成员,即亚里士多德本人!因为他是唯一称得上亚里士多德的事物,所以他是这个类别的唯一成员。
量词
值得注意的是,不存在 “所有狗” 或 “所有国家” 这样的类别。存在的是 “狗”(或 “一只狗”)和 “国家”(或 “多个国家”)这样的类别。
“所有” 被称为量词。量词是一种表示在命题中谈论某一类别多少成员的表达式。“没有”“有些” 和 “每个” 也是一些量词。
全称
命题是全称的,意味着它们的主项谈论的是该主项所指称的类别中的所有成员,而不仅仅是其中的一部分。它们表明某一类别的所有成员要么具有某个谓项所描述的属性,要么不具有该属性。
例如,比较 “所有猫都是哺乳动物” 和 “有些猫是哺乳动物”;只有第一个是全称命题,谈论的是所有猫,而不仅仅是某些特定的猫。
全称命题类型
• 全称肯定命题(所有 A 都是 B):表明某一类别(A)的所有成员同时也是另一类别(B)的成员的命题。这类命题的形式是 “所有 S 是 P”,其中 S 是主项,P 是谓项。它们有时也被称为 A 命题。
• 全称否定命题(没有 A 是 B):表明某一类别(A)的任何成员都不是另一类别(B)的成员的命题。这类命题的形式是 “没有 S 是 P”,其中 S 是主项,P 是谓项。它们有时也被称为 E 命题。
肯定与否定
一般来说,肯定就是对某事说 “是”,或认为它是真的;否定就是对某事说 “不”,或认为它是假的。全称肯定命题和全称否定命题之所以得名,是因为它们肯定或否定某个谓项对主项为真。
例如,在全称肯定命题 “所有猫都是哺乳动物” 中,我们肯定谓项 “是一种动物” 对每一只猫都为真。换句话说,我们肯定所有具有猫的属性的事物也都具有动物的属性。再换一种说法,“猫” 这一类别的每个成员同时也是 “动物” 这一类别的成员。在全称否定命题 “没有猫是爬行动物” 中,我们否定谓项 “是一种爬行动物” 对任何猫为真。换句话说,我们是说 “猫” 这一类别的任何成员都不是 “爬行动物” 这一类别的成员(反之亦然)。
命题的真假
然而,重要的是要注意,当我们称一个命题为 “肯定” 命题时,并不是说我们认可它,即认为整个命题是真的。肯定命题和否定命题的命名是根据它们对主项所表达的内容:肯定命题表明某个谓项对其主项为真,否定命题表明某个谓项对其主项为假。
例如:“所有猫都是白化动物”。因为 “猫” 这一类别的有些成员不属于 “白化事物” 这一类别。换句话说,有些猫不是白化动物,这些猫就是对“所有猫都是白化动物”的反例。从“所有猫都是白化动物”我们可以看出,肯定的陈述并不等同于真的陈述!
同样:“没有蛇是鸟”这个命题表明,否定的陈述并不等同于假的陈述!
命题可视化表示
为了更好地理解全称肯定命题和全称否定命题之间的区别,将这两种命题的含义可视化会有所帮助。为此,我们可以使用所谓的 “欧拉圆”。这是逻辑学家表示这类命题含义的一种常见方式。
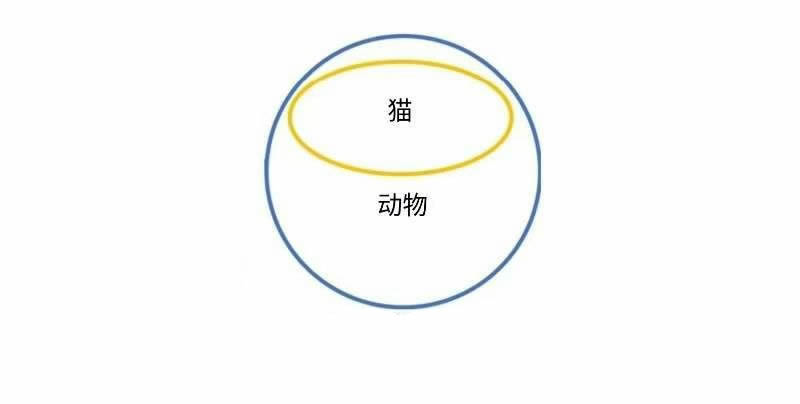
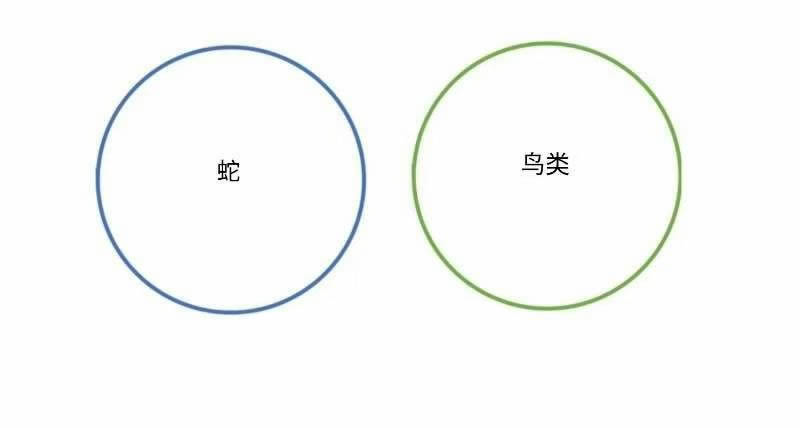
我们对世界所做的许多断言实际上都是全称肯定命题或全称否定命题的实例。因此,理解这两种类型的命题是如何起作用以及它们之间的关系是非常重要的;通过这样做,我们能更清楚地了解我们对周围世界究竟在断言什么。