体验
目标
- 描述什么是特称肯定命题和特称否定命题
- 解释每种类型的真命题和假命题之间的区别
- 判断哪些命题是每种类型命题的例子
- 用欧拉圆表示每种类型的命题
内容
特称命题类型
• 特称肯定命题(有些 A 是 B):表明某一类别(A)中的某些成员同时也是另一类别(B)中的成员的命题。其形式为 “有些 S 是 P”,其中 S 是主项,P 是谓项。
• 特称否定命题(有些 A 不是 B):表明某一类别中的某些成员不属于另一类别的命题。其形式为 “有些 S 不是 P”,其中 S 是主项,P 是谓项。
同样重要的是要注意,和全称命题一样,特称肯定命题和特称否定命题也都有真有假。我们要避免将 “肯定” 与 “真”、“否定” 与 “假” 混淆。
特称肯定
特称肯定命题:
(1)“有些猫是白化动物”
(2)“有些猫是狗”
命题(1)和(2)都是特称肯定命题的例子。然而,它们之间有一个重要的区别:(1)为真,因为事实上有些猫是白化动物(实际上占 2%!)。但(2)为假,因为猫和狗是不同的物种(一个类别的成员不会是另一个类别的成员)。
特称否定
特称否定命题:
(3)“有些蛇不是爬行动物”
(4)“有些蛇没有毒性”
命题(3)和(4)都是特称否定命题的例子。但同样,它们之间有一个重要的区别:(3)为假,而(4)为真。
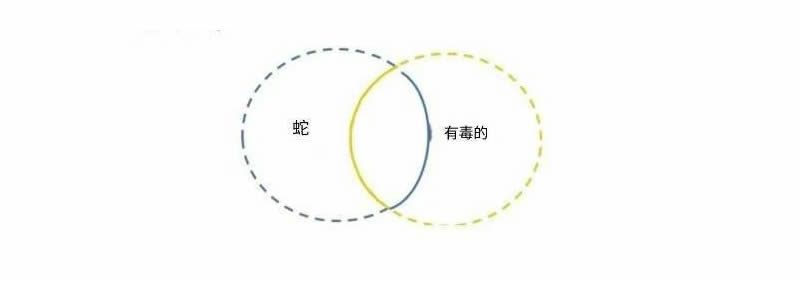
特称肯定的可视化表示
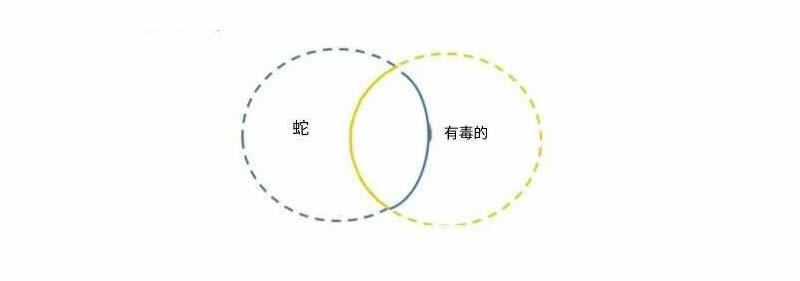
1、我们应该注意到,标有 “蛇” 的圆圈中有一部分区域包含在标有 “有毒(的动物)” 的圆圈内。这种空间关系代表特称肯定命题 “有些蛇有毒”。
2、我们可以把左边的圆圈看作包含 “蛇” 这一类别的所有成员,右边的圆圈包含 “有毒(的动物)” 这一类别的所有成员。然而,需要注意的是,如果我们只知道有些蛇有毒,那么有可能所有蛇都有毒。也就是说,如果 “所有蛇都有毒” 是真的,那么 “有些蛇有毒” 也会是真的!换句话说,如果 “蛇” 这一类别的所有成员同时也是 “有毒(的动物)” 这一类别的成员,那么 “蛇” 这一类别的某些成员同时也是 “有毒(的动物)” 这一类别的成员这一说法也会是真的。
3、由于仅从 “有些蛇有毒” 我们无法知道是否有蛇在 “有毒(的动物)” 这一类别之外,我们用虚线来补全圆圈。虚线代表未知的部分,而实线代表已知的部分。因为我们确实知道至少有一些事物既是 “蛇” 这一类别的成员,也是 “有毒(的动物)” 这一类别的成员,所以我们把 “蛇” 的圆圈中位于 “有毒(的动物)” 圆圈内的部分画成实线。此外,我们注意到,“有些蛇有毒” 为真,并且“有些有毒的动物是蛇” 也为真。因此,这个图表是对称的。也就是说,“有毒(的动物)” 圆圈的外部也是虚线。这个图表既可以表示 “有些蛇有毒”,也可以表示 “有些有毒的动物是蛇”。
所有特称肯定命题用图表表示时都会是这个样子。
特称否定的可视化表示
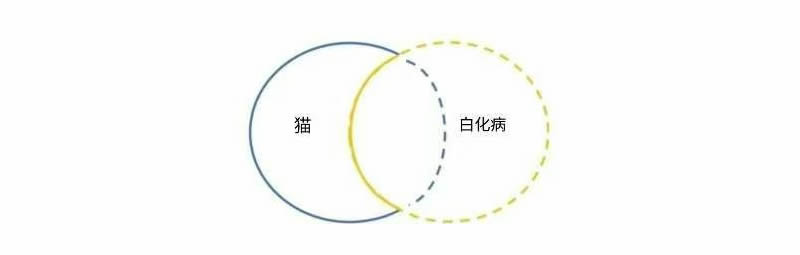
1、标有 “猫” 的圆圈中有一部分区域不包含在标有 “白化动物” 的圆圈内。这种空间关系代表特称否定命题 “有些猫不是白化动物”。因此,我们看到 “猫” 的圆圈中位于 “白化动物” 圆圈外的部分是实线。
2、然而,仅从 “有些猫不是白化动物”,我们无法知道是否有猫是白化动物!有可能存在,但根据所给信息我们无法确定。因此,我们把 “猫” 的圆圈中位于 “白化动物” 圆圈内的部分画成虚线。
3、同样,有可能 “所有白化动物都是猫”,同时 “有些猫不是白化动物” 也成立。我们只知道被实线完全包围的部分:即代表有些猫在白化动物这一类别之外的区域。
所有特称否定命题用图表表示时都会是这个样子。
就像我们对世界的许多断言是全称肯定命题或全称否定命题的实例一样,我们也做出许多属于特称肯定命题或特称否定命题的断言。
了解这些命题的运作方式以及它们之间的关系,有助于我们理解自己对周围世界究竟在表达什么。此外,将它们用图表表示出来,能帮助我们直观地理解做出这类断言时真正的含义和不包含的含义。