体验
目标
- 理解什么是矛盾关系、反对关系、全称肯定命题和全称否定命题
- 将这些关系对应到对当方阵上
- 将关于 “所有”“有些”“没有” 的知识迁移到 “总是”“有时”“从不” 上
- 理解并非所有命题都有差等命题、下反对命题或反对命题(但它们至少有其中一种)
内容
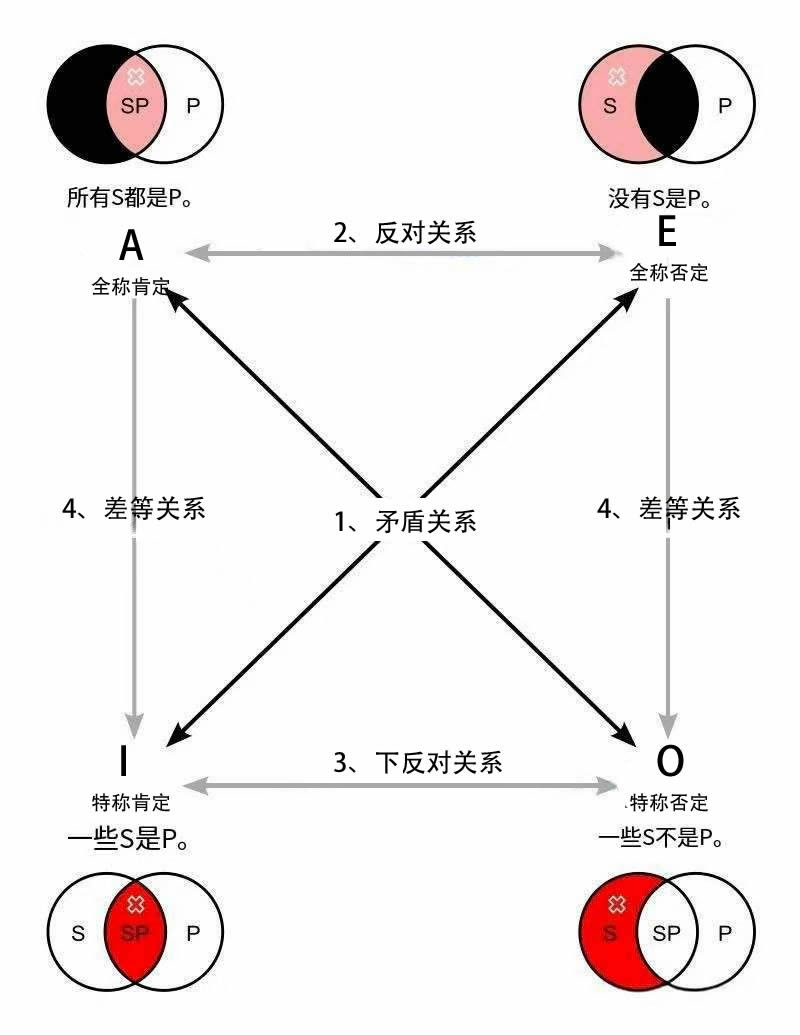
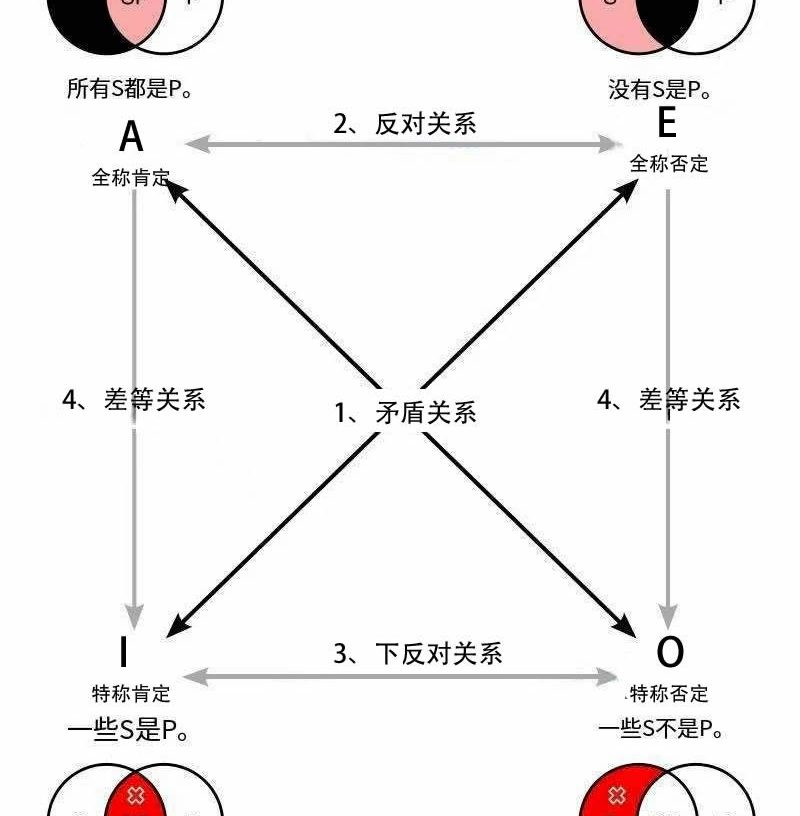
- 在这个图表中,全称肯定命题用字母 “A” 标记。全称否定命题用 “E” 标记。特称肯定命题用 “I” 标记。特称否定命题用 “O” 标记。这些都是标准惯例。
- 连接这些字母的不同线条表示上面列出的四种关系。但要记住,差等关系只是单向的。
矛盾关系
当一个命题为真时,另一个命题必为假,反之亦然,这意味着两个命题永远不可能同时为真,也不可能同时为假。
1、这种关系存在于全称肯定命题和特称否定命题之间。如果 “所有加油站都很脏”(全称肯定命题)为真,那么 “有些加油站不脏”(特称否定命题)必为假。相反,如果 “有些加油站不脏”(特称否定命题)为真,那么 “所有加油站都很脏”(全称肯定命题)必为假。

显然,其中一个命题为真意味着另一个命题为假。假设右侧图表(全称肯定命题)所呈现的内容为真。如果(全称肯定命题)为真,那么 “加油站” 这一类别的所有成员同时也是 “脏(的地方)” 这一类别的成员(因此 “加油站” 这一类别的任何成员都不是 “脏(的地方)” 这一类别之外的成员)。那么左侧的(特称否定命题)显然为假,因为它声称 “加油站” 这一类别中存在一些成员在 “脏(的地方)” 这一类别之外。
2、矛盾关系也存在于全称否定命题和特称肯定命题之间。如果 “没有 T 恤是时尚的”(全称否定命题)为真,那么 “有些 T 恤是时尚的”(特称肯定命题)必为假。相反,如果 “有些 T 恤是时尚的”(特称肯定命题)为真,那么 “没有 T 恤是时尚的”(全称否定命题)必为假。
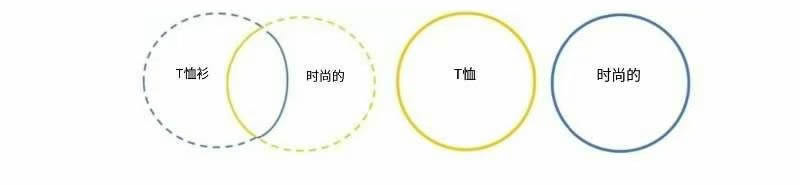
假设右侧图表(全称否定命题)为真。那么 “T 恤” 和 “时尚(的衣物)” 这两个类别之间没有重叠。那么左侧图表(特称肯定命题)显然为假,因为它表明存在这样的重叠。现在,假设(全称否定命题)为假。那么这两个类别并非完全分离(存在一些对象是这两个类别的共同成员)。那么(特称肯定命题)显然为真。
反对关系
当两个命题不能同时为真(尽管它们可以同时为假)。
这种关系存在于全称肯定命题和全称否定命题之间。“所有孩子都很可爱”(全称肯定命题)和 “没有孩子是可爱的”(全称否定命题)不能同时为真。也就是说,这两个命题可以同时为假 —— 可能有些孩子可爱,但并非所有孩子都可爱!

现在很明显,左侧(全称肯定命题)和右侧(全称否定命题)不能同时为真。“孩子” 这一类别完全包含在 “可爱(的人)” 这一类别中,同时这两个类别又完全分离,这种情况是不可能出现的。然而,(全称肯定命题)和(全称否定命题)可以同时为假。这两个类别之间可能存在重叠,这会使(全称肯定命题)和(全称否定命题)同时为假。
下反对关系
当两个命题不能同时为假(尽管它们可以同时为真)。
这种关系存在于特称肯定命题和特称否定命题之间。“有些糖果棒是免费的”(特称肯定命题)和 “有些糖果棒不是免费的”(特称否定命题)不能同时为假。不过,这两个命题有可能同时为真(要是我们生活在一个比现实更慷慨的世界里就好了!)。
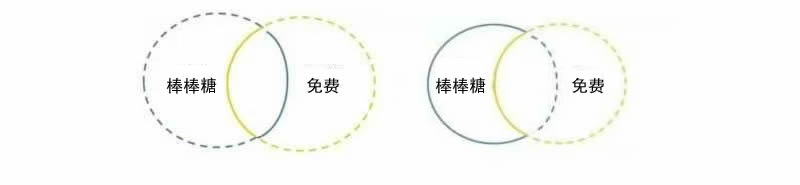
如果 “有些糖果棒是免费的”(特称肯定命题)为假,那么 “没有糖果棒是免费的”(全称否定命题)为真。同样,如果 “有些糖果棒不是免费的”(特称否定命题)为假,那么 “所有糖果棒都是免费的”(全称肯定命题)为真。
差等关系
当第一个命题为真时,第二个命题必为真(但反之则不成立)。
这种关系存在于全称肯定命题和特称肯定命题之间。如果 “所有巧克力甜点都很美味”(全称肯定命题)为真,那么 “有些巧克力甜点很美味”(特称肯定命题)也为真。但要注意 —— 如果 “有些巧克力甜点很美味”(特称肯定命题)为真,并不一定意味着 “所有巧克力甜点都很美味”(全称肯定命题)也为真!这意味着(特称肯定命题)是(全称肯定命题)的差等命题,但反之则不然。换句话说,(特称肯定命题)没有差等命题。
这种关系也存在于全称否定命题和特称否定命题之间。如果 “没有青少年是早起的人”(全称否定命题)为真,那么 “有些青少年不是早起的人”(特称否定命题)也为真。然而,“有些青少年不是早起的人”(特称否定命题)为真,并不意味着 “没有青少年是早起的人”(全称否定命题)也为真。