体验
目标
- 能够构建和识别遵循肯定前件式和否定后件式规则的论证
内容
假言命题的前件与后件
假言命题是由两个命题通过 “前件的真蕴含后件的真” 这一断言连接起来。
这种命题的形式是 “如果 p,那么 q”。例如:“如果纽约下雪,那么纽约的温度低于 32 摄氏度”。
前件:假言命题中出现的两个命题中的第一个命题。在上述例子中,前件是 “纽约下雪”。
后件:假言命题中出现的两个命题中的最后一个命题。在上述例子中,后件是 “纽约的温度低于 32 华氏度”。
假言命题的肯定前件式
一条推理规则,它指出如果一个假言命题 “如果 p,那么 q” 为真,且前件 “p” 为真,那么后件 “q” 为真。在变项符号表示中,该规则的形式如下:
(1)如果 p,那么 q
(2)p
(3)因此,q
假言命题的否定后件式
一条推理规则,它指出如果一个假言命题 “如果 p,那么 q” 为真,且后件 “q” 为假,那么前件 “p” 为假。在变项符号表示中,该规则的形式如下:
(1)如果 p,那么 q
(2)非 q
(3)因此,非 p
直言命题的肯定前件式
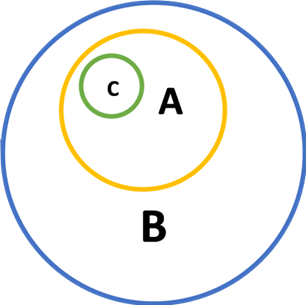
当(a)某个范畴 A 中的所有成员都是另一个范畴 B 中的成员,且(b)某个事物(或某些事物)C 是范畴 A 中的成员时,适用此规则。由此可推出,C 是范畴 B 中的成员。
(1)所有 A 都是 B
(2)C 是 A / 所有 C 都是 A
(3)因此,C 是 B / 所有 C 都是 B
直言命题的否定后件式
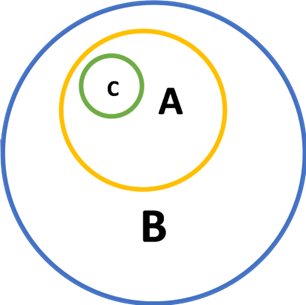
当(a)某个范畴 A 中的所有成员都是另一个范畴 B 中的成员,且(b)某个事物(或某些事物)C 不是范畴 B 中的成员时,适用此规则。由此可推出,C 不是范畴 A 中的成员。
(1)所有 A 都是 B
(2)C 不是 B / 没有 C 是 B
(3)因此,C 不是 A / 没有 C 是 A
现实世界中的肯定前件式
假设《罪与罚》这本陀思妥耶夫斯基的书在你房间里你最喜欢的书架上。你哥哥走进你的房间说,你最喜欢的书架上的所有书都是他最喜欢的书。你(通过肯定前件式)推断《罪与罚》是你哥哥最喜欢的书之一。
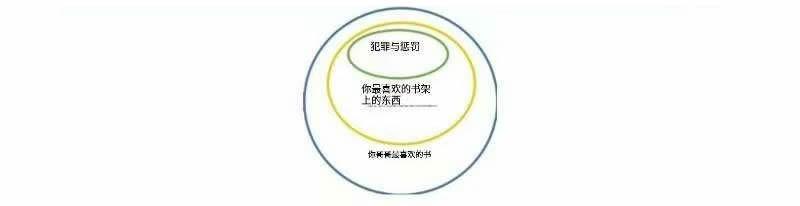
三段论形式的肯定前件式
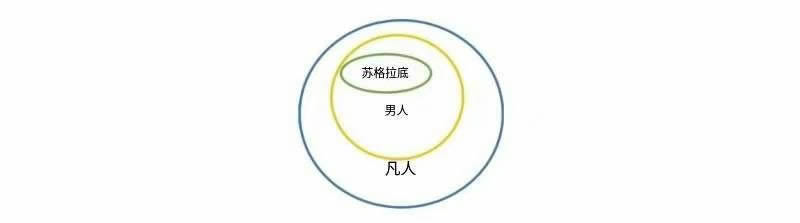
(1)所有男人都是凡人(所有 A 都是 B)
(2)苏格拉底是男人(C 是 A)
(3)因此,苏格拉底是凡人(因此,C 是 B)
现实世界中的否定后件式
假设你知道任何学过亚里士多德逻辑的人都会知道亚里士多德是谁。你问你的朋友是否知道亚里士多德,她说不知道。你推断她没有学过亚里士多德逻辑。
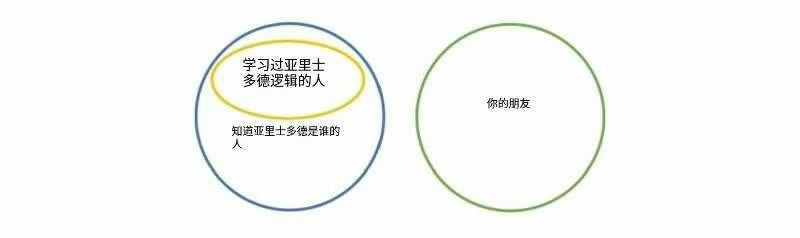
三段论形式的否定后件式
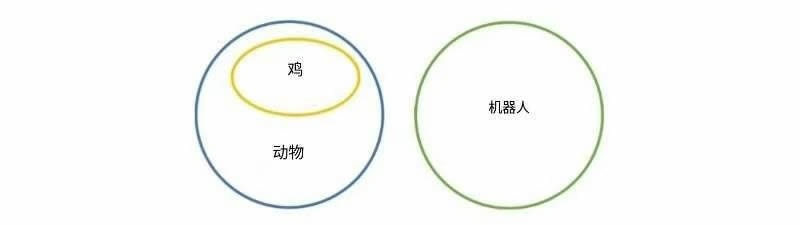
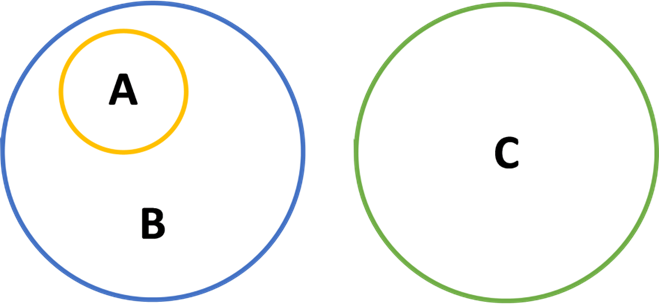
(1)所有鸡都是动物(所有 A 都是 B)
(2)没有机器人是动物(C 不是 B)
(3)因此,机器人不是鸡(因此,C 不是 A)