我们前面已经证明,人人都有一身甚至连自己都不知道的能耐,我们不以为意的对事物大小的观察居然就能推导出多维世界物体的“面积”!
然而,说到剪纸,几乎没有谁还能产生足够的兴趣。毕竟,国学都带着老旧的标签。
可是,现在开始,我希望你能够给剪纸、也给自己一个机会,了解它蕴藏着的神奇世界!
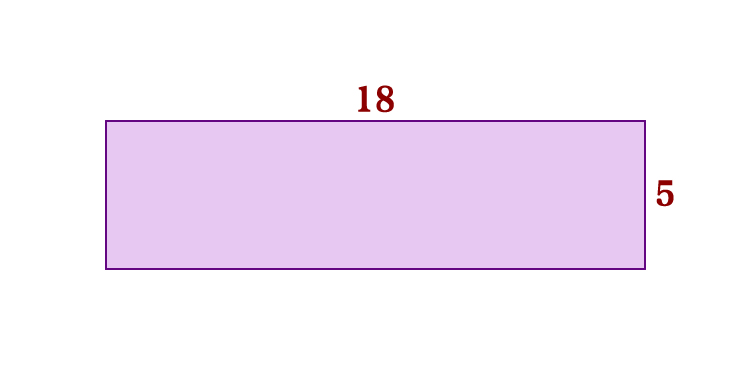
横着剪
比如:
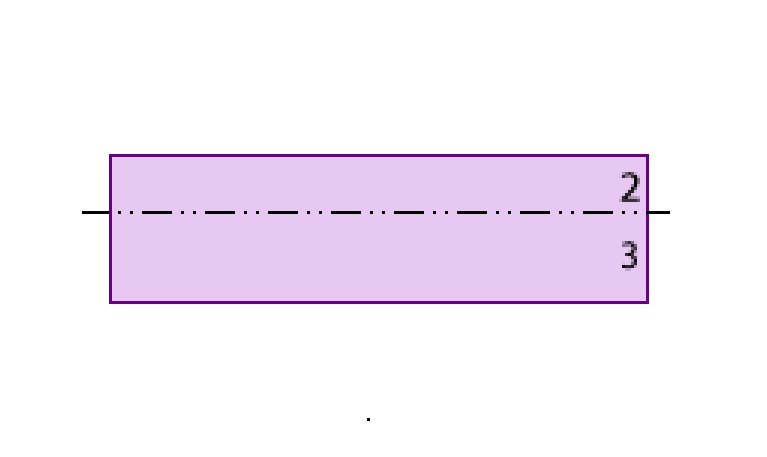
根据纸张大小在裁剪前后并没有发生变化,我们可以确定:\(18 \times 5 = 18 \times \left(2 + 3\right) = 18 \times 2 + 18 \times 3\)。
竖着剪
比如:
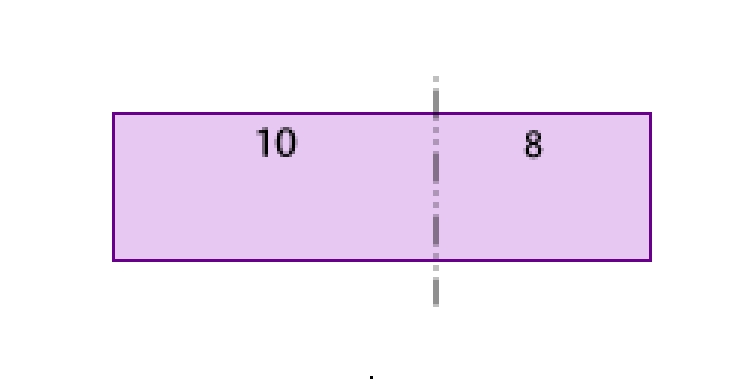
根据结果,我们也可以确定:\(18 \times 5 = \left(10 + 8\right) \times 5 = 10 \times 5 + 8 \times 5\)。
随机操作
按指定大小来裁剪确实有些费劲,有些人还可能因为熟练度的问题产生裁剪误差。不过,这并不重要。
接下来让我们做得随意一些(无需思考精确的长度问题),比如:
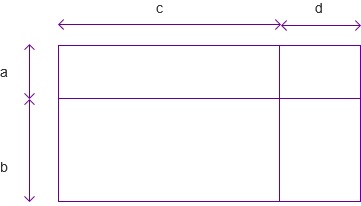
这就意味着:
\(\left(a + b\right) \cdot \left(c + d\right) = a \cdot c + a \cdot d + b \cdot c + b \cdot d\)
特殊化
如果你用的是正方形的纸,横竖边做相同的分割a+b时,
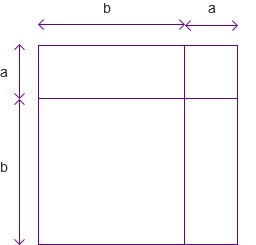
就能得到这样的结果:
\(\left(a + b\right)^2 = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2\)
复杂化
这时候,你甚至可以放飞自我,不再按照特定指示裁剪。比如横竖多剪一次,又能有什么问题呢
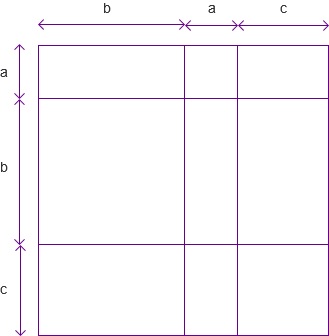
(\left(a + b + c\right)^2 = a^2 + ab + ac + b^2 + ba + bc + c^2 + ca + cb = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)
斜着裁剪
哦!好吧,你甚至在试着斜着裁剪(按相同大小剪去正方形的纸的角):
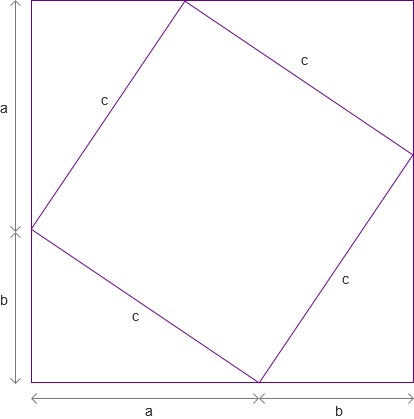
\(\left(a + b\right)^2 = 4 \bigtriangleup + c^2\),这是什么鬼?
如果你并不知道三角形的面积计算方法时,你可以通过组合发现,这四个三角形可以两两拼合成相等的2个长方形,于是:
\(\left(a + b\right)^2 = 2ab + c^2 \Rightarrow a^2 + 2ab + b^2 = 2ab + c^2\mathop{\Rightarrow}\limits^{同减2ab}a^2 + b^2 = c^2\)(这便是鼎鼎大名的勾股定理!)。
三维推广
如果凑巧你的面前有一个方块状豆腐,而一旁有把菜刀,你就可以试试对长宽高做一下相同的分割,你能得到一些豆腐粒:
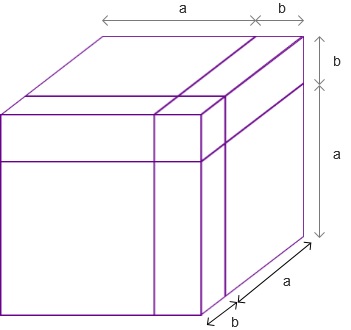
小心地比较一下各个豆腐粒的大小,可以知道:
\(\left(a + b\right)^3 = a^3 + 3a^2b + 3ab^2 + b^3\)
现在,你已经看到,只要稍加留意,小小手工就可以揭示出那些看似深奥的知识。

